Header logo is am

On the Design of LQR Kernels for Efficient Controller Learning

2017

Conference Paper

am

ics

pn

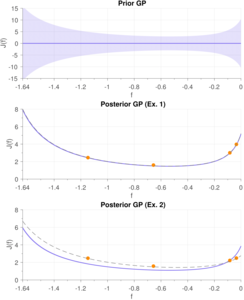
Finding optimal feedback controllers for nonlinear dynamic systems from data is hard. Recently, Bayesian optimization (BO) has been proposed as a powerful framework for direct controller tuning from experimental trials. For selecting the next query point and finding the global optimum, BO relies on a probabilistic description of the latent objective function, typically a Gaussian process (GP). As is shown herein, GPs with a common kernel choice can, however, lead to poor learning outcomes on standard quadratic control problems. For a first-order system, we construct two kernels that specifically leverage the structure of the well-known Linear Quadratic Regulator (LQR), yet retain the flexibility of Bayesian nonparametric learning. Simulations of uncertain linear and nonlinear systems demonstrate that the LQR kernels yield superior learning performance.

Author(s): Alonso Marco and Philipp Hennig and Stefan Schaal and Sebastian Trimpe
Book Title: Proceedings of the 56th IEEE Annual Conference on Decision and Control (CDC)
Pages: 5193--5200
Year: 2017
Month: December
Day: 12-15
Publisher: IEEE
Department(s): Autonomous Motion, Intelligent Control Systems, Probabilistic Numerics
Research Project(s): Controller Learning using Bayesian Optimization
Bibtex Type: Conference Paper (conference)
Paper Type: Conference
DOI: 10.1109/CDC.2017.8264429
Event Name: IEEE Conference on Decision and Control
Event Place: Melbourne, VIC, Australia
State: Published
Links: arXiv
PDF
On the Design of LQR Kernels for Efficient Controller Learning - CDC presentation
Video:

BibTex 

@conference{MaHeScTr17,
  title = {On the Design of {LQR} Kernels for Efficient Controller Learning},
  author = {Marco, Alonso and Hennig, Philipp and Schaal, Stefan and Trimpe, Sebastian},
  booktitle = {Proceedings of the 56th IEEE Annual Conference on Decision and Control (CDC)},
  pages = {5193--5200},
  publisher = {IEEE},
  month = dec,
  year = {2017},
  month_numeric = {12}
}