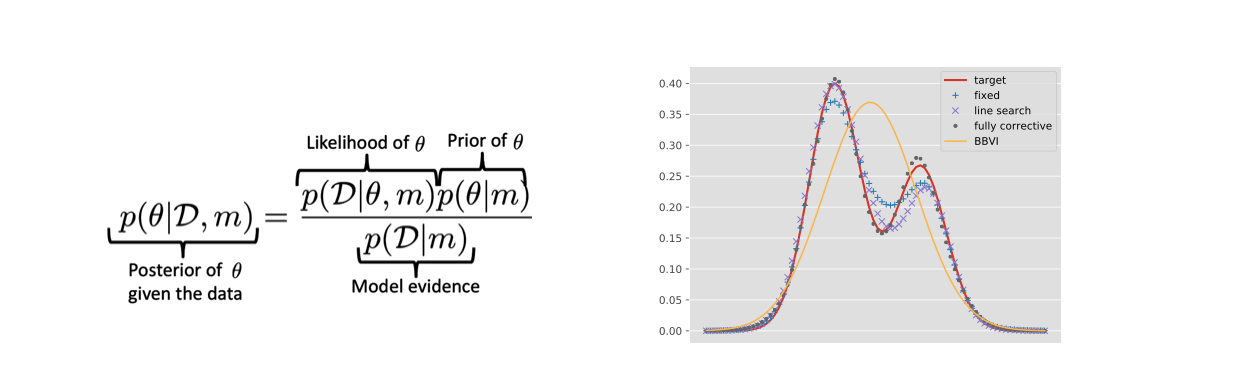
Left: Illustration of probabilistic inference. Right: Comparison between black box variational inference (BBVI) and three variants of our boosting BBVI method on a mixture of Gaussians~[ ].
The probabilistic formulation of inference conditions probability measures encoding prior assumptions by multiplying with a likelihood of the data given the generative process. It remains one of the main research streams within machine learning.
Nonparametric inference on function spaces Gaussian Process models allow for non-parametric inference in function spaces. They have a strong inductive bias specified by the kernel function between observations, which allows for data-efficient learning. One of our main themes in this field has been nonparametric inference on function spaces using Gaussian process models, with its main practical challenge for inference being the cubic complexity in terms of the number of training points.
We provided an analysis of two classes of approximations~[ ], and explored kernels that can account for invariances between data points~[ ]. To this end, we construct a kernel that explicitly takes these invariances into account by integrating over the orbits of general symmetry transformations. We provide a tractable inference scheme that generalises recent advances in Convolutional Gaussian Processes.
In work on the Mondrian kernel~[ ], we provide a new algorithm for approximating the Laplace kernel in any kernel method application (including in Gaussian processes) using random features. Attractive properties of the algorithm include that it allows finding the best kernel bandwidth hyperparameter efficiently and it is well-suited for online learning.
Variational Inference We studied the convergence properties of Boosting Variational inference from a modern optimization viewpoint~[ ]. We subsequently generalized this approach [ ] by showing that boosting variational inference satisfies a relaxed smoothness assumption, leading to richer posterior approximations (see Fig. 2).
Inference on discrete graphical models An open challenge is to perform efficient inference in discrete graphical models. We showed that the popular Gumbel trick is just one method out of an entire family and that other methods can work better [ ] (Best Paper Honourable Mention at ICML 2017). We developed a sampling-based Bayesian inference algorithm ~[ ] for the infinite factorial finite state machine model.
Probabilistic programming languages aim to enable data scientists to express probabilistic models without needing to worry about the inference step. We presented an architectural design and a performant implementation of a probabilistic programming library [ ]. We showed how to conceptualise inference as manipulating representations of probabilistic programs [ ], and studied how to represent distributions of functions of random variables [ ] with kernel mean embeddings.
