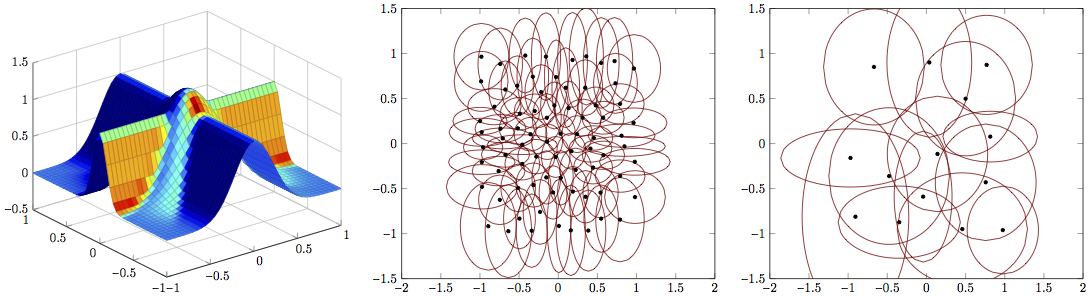
Comparing local regression methods: traditional locally weighted regression (which trains local models independently), and local Gaussian regression (in which local models are trained collaboratively). Training data was drawn from 2D cross function (left). Local models learned by locally weighted regression (middle) and by local Gaussian regression (right) are shown.
Besides accuracy and sample efficiency, computational cost is a crucial design criterion for machine learning algorithms in real-time settings, such as control problems. An example is the modeling of robot dynamics: The sensors in a robot can produce thousands of data points per second, quickly amassing a coverage of the task related workspace, but what really matters is that the learning algorithm incorporates this data in real time, as a physical system can not necessarily stop and wait in its control. Thus, a learning method in such settings should produce a good local model in fractions of a second, and be able to extend this model as the robot explores new areas of a very high dimensional workspace that can often not be anticipated by collecting “representative” training data.
In robotics, local learning approaches such as locally weighted regression have thus been favored over global approaches such as Gaussian process regression in the past. In this context we are investigating
- Approaches that combine robust learning frameworks such aus Gaussian process regression with local model learning approaches [ ].
- How to efficiently and robustly learn the neighborhood of a local model.
- Regression algorithms that can learn continously on highly correlated data.
To address these research problems, we look at local learning approaches from a probabilistic perspective such that we can include prior information regarding model parameters in a principled manner and attach uncertainty estimates to predictions. Furthermore, we explore the use of variational inference to reduce computational complexity when necessary.
